Hacheur Abaisseur – Théorie

Last updated on 7 décembre 2025

Mais comment ça fonctionne ?

Dans cet article étudions le schéma de base du hacheur abaisseur pour en comprendre son fonctionnement.

Un grand merci à Jean-François Sautreau, enseignant à l’IUT de Troyes, qui m’a transmis sa passion de l’électronique de puissance.

Cet article est fortement inspiré de son cours d’Energie.

Hypothèses et Approximations

Dans toute la suite nous partirons des principes suivants :

• Tous les composants sont supposés parfaits (par exemple la tension au borne de la diode est nulle lorsqu’elle conduit)
• L’interrupteur est rapide, son temps de commutation est négligeable devant la période de travail.
• Le courant ne s’annule jamais car l’inductance et la fréquence de découpage sont correctement dimensionnées.

Schéma du hacheur

Voici le schéma de base du hacheur dont nous allons parler dans la suite :

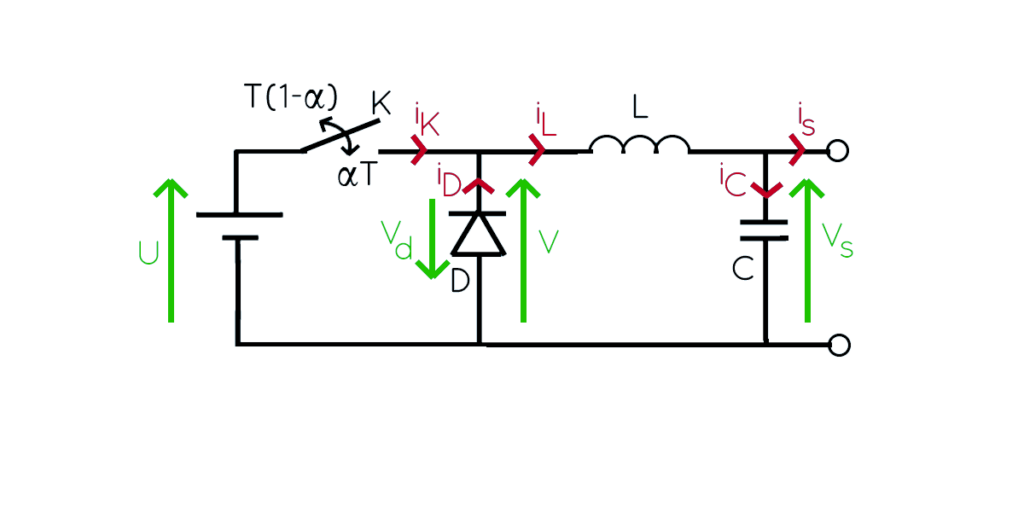
Sur ce schéma on note α le rapport cyclique de l’interrupteur K c’est-à-dire la proportion de la période T durant laquelle K est fermé. Par conséquent 0 < α < 1.

Par ailleurs T = 1/f avec f la fréquence de découpage.

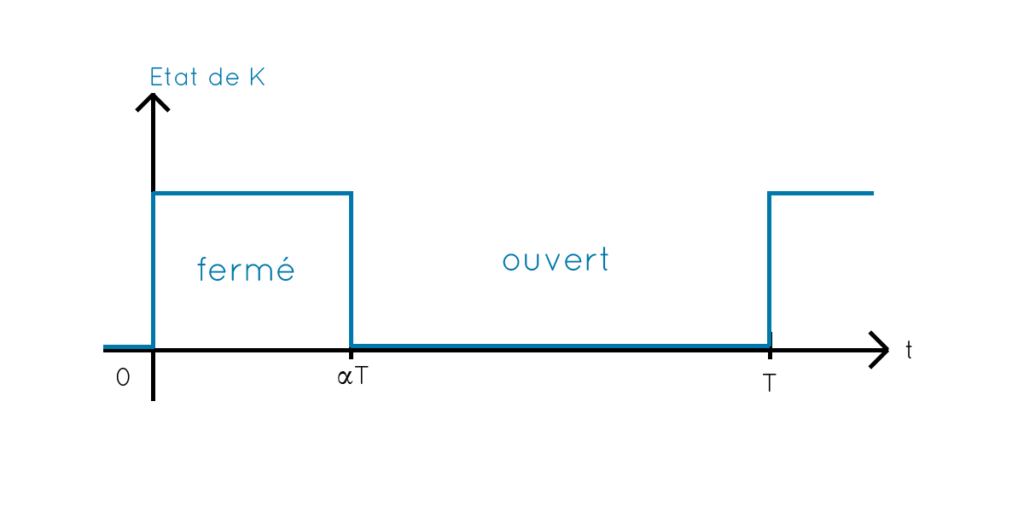
Pour étudier ce circuit il faut traiter indépendamment les deux cas : interrupteur ouvert et interrupteur fermé.

Lorsque l’interrupteur est fermé

Lorsque l’interrupteur se ferme v=u, donc v_d=-u<0 par conséquent la diode est bloquée.
Puisque la diode est bloquée i_d=0 donc i_L=i_K.

Par ailleurs v=u=L\times\frac{di_L}{dt} + v_s.
Remarque : on considère v_s constante sur toute la période car le condensateur à une valeur suffisante.

Avec la dernière équation on obtient :

\frac{di_L}{dt} = \frac{u-v_s}{L} \Rightarrow \boxed{i_L=\frac{u-v_s}{L}t+k}  

comme v_s<u le courant augmente linéairement.

Lorsque l’interrupteur est ouvert

Dans la seconde partie de la période, puisque K est ouvert on a i_K=0 on en déduit que i_L=i_d comme vu dans les hypothèses ce courant ne peut pas s’annuler donc la diode conduit ce qui nous donne v_d=-v=0.

v=0=L\frac{di_L}{dt}+v_s \Rightarrow \frac{di_L}{dt} = \frac{-v_s}{L} \Rightarrow \boxed{ i_L = \frac{-v_s}{L}t + k'}

Synthèse sur la période

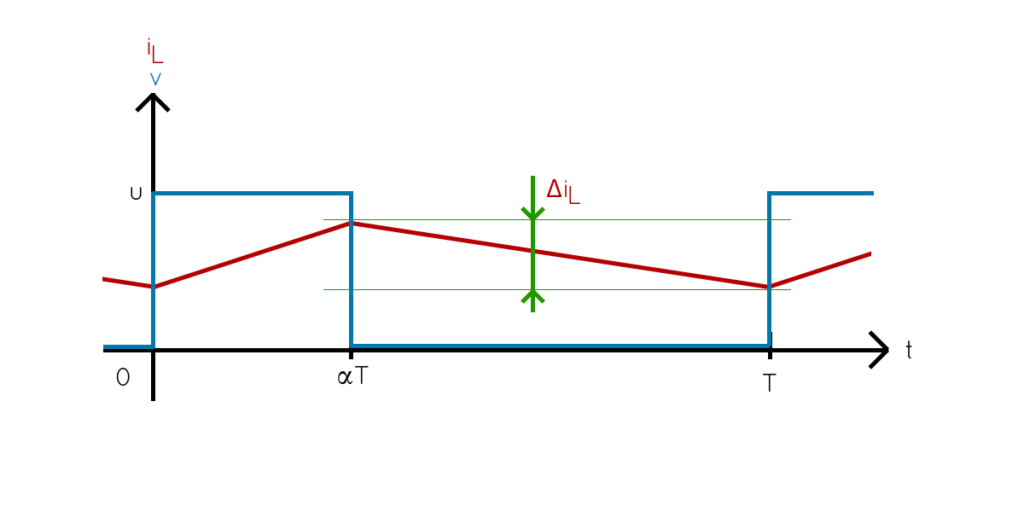
A partir de ces informations nous allons pouvoir trouver v_s.
Pour cela il faut exploiter la propriété suivante : {v_L}_{moy}= 0 sur une période.

v - v_L -v_s =0 \Rightarrow v_{moy} = v_s

v_{moy} = \frac{1}{T} \int_{0}^{T}v.dt=\frac{\text{aire de v}}{T} = \frac{u\times\alpha T}{T}

\boxed{v_s=\alpha u}

Comme 0<\alpha<1 \Rightarrow 0\leq v_s \leq u on obtient une tension inférieure à celle d’entrée.

Nous sommes maintenant capable de régler la valeur de v_s en agissant simplement sur le rapport cyclique \alpha.

Conclusion

A partir de composants de base de l’électronique nous avons réussi à réaliser un hacheur abaisseur dont la commande se fait simplement en jouant sur le rapport cyclique d’ouverture d’un interrupteur.

Bien évidemment dans un cas réel l’interrupteur sera remplacé par un transistor (par exemple).

Dans le prochain article, tentons de réaliser une alimentation pour expérimenter la partie commande de l’interrupteur. C’est de loin la partie la plus complexe de ce hacheur.
Nous pourrons essayer différentes méthodes de contrôle.